La aparición del cálculo diferencial fue el final de un largo recorrido que comenzó con los métodos de resolución de problemas de cálculo de cuadraturas en la antigua Grecia y que prosiguió con las nuevas teorías y problemas que durante el Renacimiento aparecieron.
El movimiento fue el objeto de estudio por excelencia durante los siglos XV al XVII, comenzando por el movimiento de los planetas, las investigaciones se trasladaron rápidamente también al movimiento de objetos sobre la Tierra.
El estudio del movimiento planteaba un cambio de paradigma que los matemáticos de la época tuvieron que realizar, estudiar el movimiento significa cuantificar magnitudes continuas en contraposición a la interpretación del movimiento de los antiguos griegos que trataban únicamente con magnitudes discretas.
Hoy en día, vemos con total naturalidad los movimientos de cuerpos como funciones dependientes del tiempo, sin embargo, en el siglo XIV no se tenía claro ni siquiera el concepto de función.
Cuatro grandes problemas promovieron el desarrollo del cálculo diferencial: conocer la velocidad y aceleración de un cuerpo, conocer la dirección de un proyectil en cualquier punto de su trayectoria, conocer los máximo y mínimos de una trayectoria y conocer la longitud de determinadas curvas.
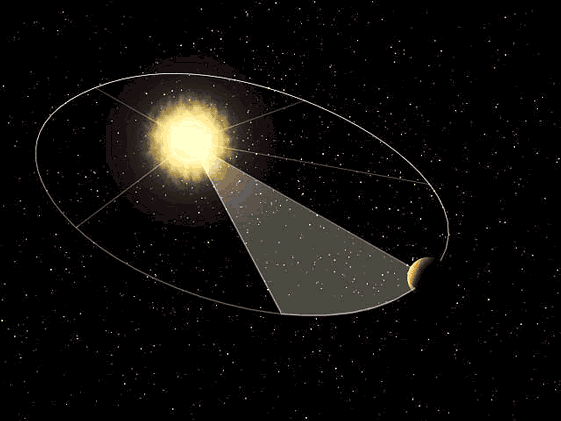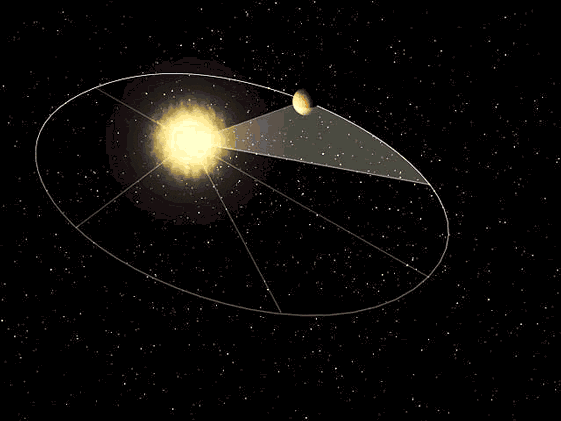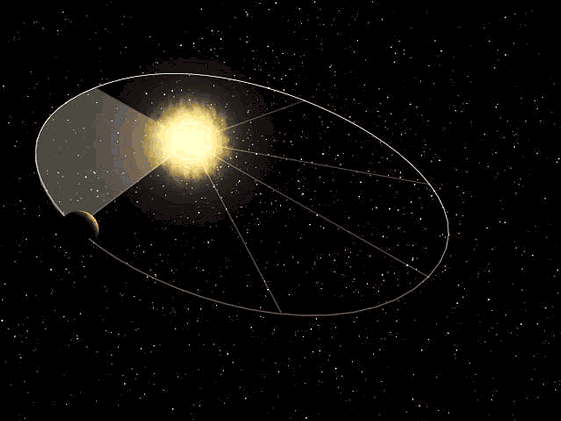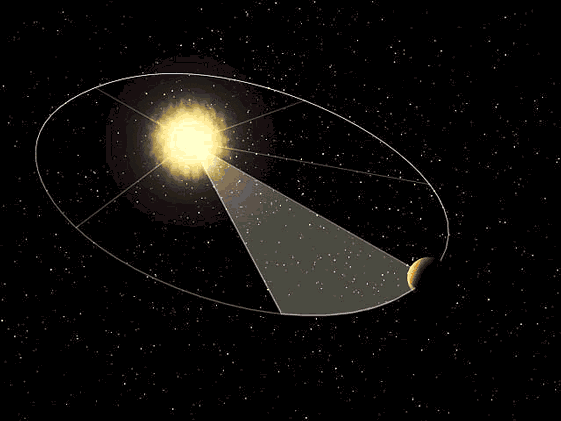
Kepler en su tercera ley argumentaba que el tiempo que tarda un planeta en dar la vuelta al sol es directamente proporcional al cubo de la longitud del semieje mayor de su órbita, para realizar ciertas comprobaciones fue necesario conocer la distancia que recorrían los planetas en un determinado periodo de tiempo, eso exigía conocer por ejemplo la longitud de un arco de elipse.
La longitud de curvas también apareció en escena con la relectura de los trabajos griegos, pues ya Arquímedes, Euclides, Apolonio, etc. habían intentado hallar la longitud de determinadas curvas, son los denominados problemas de cuadraturas cuyo método principal de cálculo era el método exhaustivo.
Método exhaustivo
Este método de aproximación sucesiva fue usado para calcular áreas y volúmenes desde la época de Arquímedes, aplicando la subdivisión infinita.
Original de Eudoxo, se fundamenta en el siguiente lema:
“Dadas magnitudes cualesquiera a > 0 y b > 0, siempre es posible, por pequeña que sea a y grande que sea b, conseguir que un múltiplo conveniente de a exceda a b, es decir na > b para algún número natural n.”
Este lema, es la base de la proposición que afirma:
“Si de cualquier magnitud sustraemos una parte no menor que su mitad, y si del resto sustraemos de nueva una cantidad no menor que su mitad, y si continuamos repitiendo este proceso de sustracción, terminaremos por obtener como resto una magnitud menor que cualquier magnitud del mismo tipo dada de antemano”
En términos actuales, la proposición afirma que dada una magnitud M y una e otra magnitud del mismo tipo y r un número tal que \( \frac{1}{2} <r<1\) podemos encontrar un número N tal que \(M(1-r)^N<e\).
En esta proposición se basa el método exhaustivo.
Veamos un ejemplo. En una carta que Arquímedes le escribe Dositheus, le muestra como consigue la cuadratura de una parábola usando el método exhaustivo.
Arquímedes definía el triángulo AVB, llamado triángulo inscrito.
Posteriormente dividía en cuatro partes el segmento AB, obteniendo los triángulos AMV y VNB. Arquímedes demuestra la siguiente relación entre las áreas de los triángulos VNB y VCB.
\[A_{VNB}= \frac{1}{4} A_{VCB}\]
\[A_{AMV}=\frac{1}{4} A_{ACV}\]
Y establece que \[A_{VNB} + A_{AMV} = \frac{1}{4} A_{AVB}\]
Si repetimos el proceso:
Pero Arquímedes no sabía sumar series infinitas pero sí sabía el principio de Eudoxo y lo aplica de forma magistral. Veamos
Sea S el área del segmento parabólico AVB.
Supongamos que \(S- \frac{4}{3}A>0\).
Aplicando el principio de Eduxo en el sentido de que el área A es mayor que la mitad del área del segmento parabólico, tenemos:
\[S, S-A, S- ( A+ \frac{1}{4}A), S – (A+\frac{1}{4} A+ \frac{1}{16} A), …, S – (A+\frac{1}{4} A+ \frac{1}{16} A+ ⋯+\frac{1}{4^n} A )\]
En virtud del principio,
\[S- \frac{4}{3} A> A+\frac{1}{4} A+ \frac{1}{16} A+ ⋯+\frac{1}{4^n} A\]
Expresión que entra en contradicción con el hecho de que la suma finita:
\[A + \frac{1}{4} A+\frac{1}{16} A+ \frac{1}{32} A+ ⋯+\frac{1}{4^n} A \]
es
\[ \frac{4}{3}A - \frac{1}{3} \frac{1}{4^n}A\]
Por tanto,
\[S- \frac{4}{3} A < A + \frac{1}{4} A+\frac{1}{16} A+ \frac{1}{32} A+ ⋯+\frac{1}{4^n} A\]
En contra de nuestra hipótesis inicial. Arquímedes llegó a la conclusión de qué \(S- \frac{4}{3} A>0\) no podía ser.
Supuso por tanto que que \(S- \frac{4}{3}A<0\). Un razonamiento similar le llevó a la misma conclusión,\(S- \frac{4}{3} A<0\) no podía ser.
La única posibilidad es que que \(S- \frac{4}{3}A=0\) y por tanto que \[S= \frac{4}{3} A\]